Numerical Solution

For computations, the analysis equations (1)-(3), (8), (9) were re-written in the non-conservative form using pressure P, enthalpy H and velocity V as flow variables. The Gruneisen parameter f and isentropic speed of sound c were introduced in the equations [1]. Using the basic thermodynamic identity

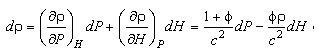
the equations (1)-(3) are transformed to the form

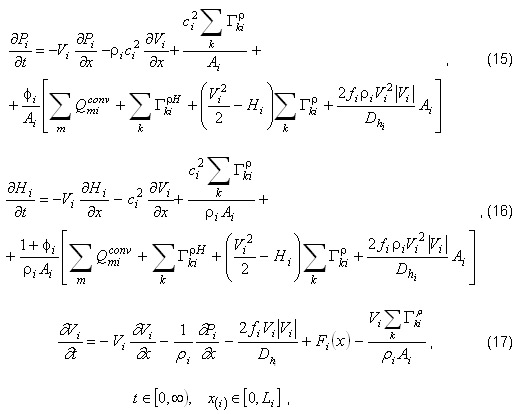
where

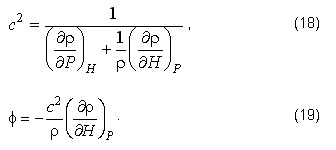
Equations (8) and (9) are re-written as

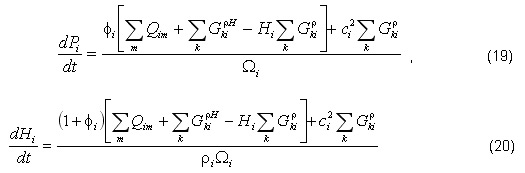
So, the time derivatives for different helium parameters are separated and assigned in explicit form.

All equations related to channels and conductors are represented via finite differences with respect to the space variable x using the following approximation for the first and second order derivatives in a mesh node "i"

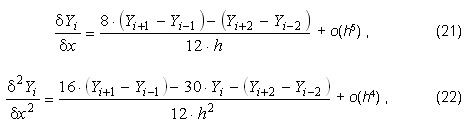
where h is a step of uniform spatial discretization. A special attention is paid to approximation of derivatives in the boundary nodes. In VENECIA, this approximation is significantly improved and allows provide stable calculation for very fast process at the boundaries (explosion of pipe etc.). As a result of such discretization procedure, the initial system of three partial differential equations for the P-H-Vchannel parameters is transformed into 3N ordinary differential equations for the parameters in the mesh nodes with respect to time.

The number of steps (nodes) on the space variable x is arbitrary and individual for each channel. For thechannels coupled by heat and mass transfer in the longitudinal direction the number of nodes should be identical.

where t is the time step for integration.

The numerical method for solving equation (14) is based on a semi-explicit spliting-up method for parabolic partial differential equations [3].